※ 이 글은 코드 위주이니 설명은 아래 링크 확인 !
※ C AVL 트리(AVL Tree) 설명
C AVL 트리(AVL Tree) 설명
※ 트리의 개념과 이진탐색트리를 포함해서 설명이 진행되므로 모르면 아래 링크로 확인 ! ※ C 트리(Tree)설명 C 트리(Tree) 설명 트리 - 비선형 자료구조의 일종이다. - 계층적 관계(Hierarchical Relatio
srdeveloper.tistory.com
AVL 트리에 사용할 구조체
typedef struct Node
{
int data;
struct Node* Parent, * Left, * Right;
}Node;
※ 이전 이진탐색트리와는 다르게 코드의 간결함을 위해 부모 노드를 참조할 변수를 하나 더 만든다.
균형 인수(Balance Factor) 구하기
- 균형 인수 = 왼쪽 서브 트리의 높이 - 오른쪽 서브트리의 높이
int GetHeight(Node* node)
{
if (node == NULL) return 0;
int leftDepth = GetHeight(node->Left);
int rightDepth = GetHeight(node->Right);
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
int CalculateBalanceFactor(Node* node)
{
return GetHeight(node->Left) - GetHeight(node->Right);
}
※ 균형 인수는 CalculateBalanceFactor를 호출하면 된다.
※ GetHeight는 재귀함수로 구성해서 단말노드까지의 높이를 반환한다.
LL(Left Left), RR(Right Right)
Node* LL(Node* node)
{
Node* childNode = node->Left;
node->Left = childNode->Right;
if (childNode->Right != NULL)
childNode->Right->Parent = node;
childNode->Right = node;
childNode->Parent = node->Parent;
node->Parent = childNode;
return childNode;
}
※ LL은 다음과 같은 순서로 진행된다.
1. Child node(이하 CNode)의 오른쪽 자식 참조를 Parent node(이하 PNode)의 왼쪽 자식으로 넣어준다.
※ 이 때 CNode의 오른쪽 자식 노드가 NULL이 아니면 오른쪽 자식노드의 부모 참조를 PNode로 변경해준다.
2. CNode의 오른쪽 자식으로 PNode를 넣어준다.
3. CNode가 PNode의 위치와 바뀌므로 CNode의 부모 참조를 PNode의 부모로 변경해준다.
4. PNode의 부모는 CNode가 되므로 PNode의 부모 참조를 CNode로 변경해준다.
※ RR은 LL의 순서를 반대로 해주면 된다.
LR(Left Right) RL(Right Left)
Node* LR(Node* node)
{
node->Left = RR(node->Left);
return LL(node);
}
※ LR은 다음과 같은 순서로 진행된다.
1. Parent node(이하 PNode)의 왼쪽 자식 노드를 RR회전 해준다.
2. PNode를 LL회전 해준다.
※ RL은 LR의 순서를 반대로 해주면 된다.
AVL 리밸런싱
- AVL의 균형을 맞추는 함수는 다음과 같이 작성하면 된다.
Node* AVLSet(Node* node)
{
int depth = CalculateBalanceFactor(node);
if (depth >= 2)
{
depth = CalculateBalanceFactor(node->Left);
if (depth >= 1)
{
//LL : Left Left
node = LL(node);
}
else
{
//LR : Left Right
node = LR(node);
}
}
else if (depth <= -2)
{
depth = CalculateBalanceFactor(node->Right);
if (depth <= -1)
{
//RR : Right Right
node = RR(node);
}
else
{
//RL : Right Left
node = RL(node);
}
}
return node;
}
※ 어떤 서브트리의 부모노드를 대상으로 균형 인수를 구한다. (절대값이 2차이가 나면 균형을 잡아준다.)
※ 이 때, CalcualteBalanceFactor함수에서 왼쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺴고있으니 반환값이 양수면 왼쪽 서브트리, 음수면 오른쪽 서브트리의 높이가 높다는 것이다.
※ 균형 인수의 절대값이 2가 되면 높이가 높은 서브트리를 대상으로 균형 인수를 한번더 계산해서 서브트리가 LL상태(혹은 RR)인지 LR상태(혹은 RL)상태인지 알아본 뒤, 상태에 따라 알맞은 함수를 적용해서 리밸런싱을 진행한다.
자, 여기까지 이해를 했다면 일단 AVL 트리의 리밸런싱 코드는 끝이났다.
이걸 어떤 타이밍에 적용해줘야 할까? 답은 트리에 변경점이 발생하는 시점이다.
즉, 데이터를 추가(Insert) 할 때, 데이터를 삭제(Delete) 할 때 위의 함수를 넣어주면 된다. 이점을 잘 생각해서 다음 풀 소스코드를 이해해보자. (이번엔 양이 양인만큼 코드가 길다.)
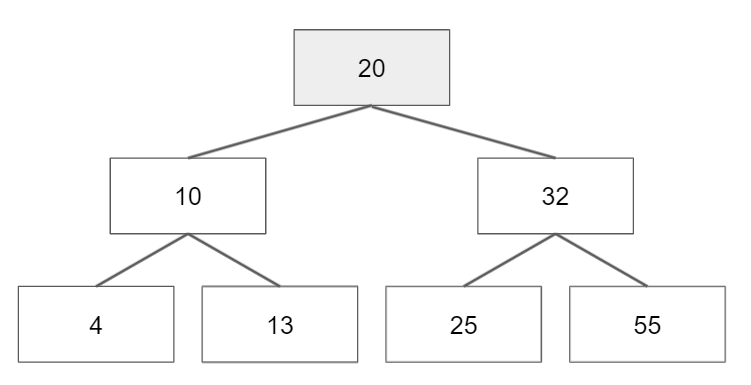이번 코드에 활용할 트리 구조
#include <stdio.h>
typedef struct Node
{
int data;
struct Node* Parent, * Left, * Right;
}Node;
int GetHeight(Node* node)
{
if (node == NULL) return 0;
int leftDepth = GetHeight(node->Left);
int rightDepth = GetHeight(node->Right);
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
int CalculateBalanceFactor(Node* node)
{
return GetHeight(node->Left) - GetHeight(node->Right);
}
Node* RR(Node* node)
{
Node* childNode = node->Right;
node->Right = childNode->Left;
if (childNode->Left != NULL)
childNode->Left->Parent = node;
childNode->Left = node;
childNode->Parent = node->Parent;
node->Parent = childNode;
return childNode;
}
Node* LL(Node* node)
{
Node* childNode = node->Left;
node->Left = childNode->Right;
if (childNode->Right != NULL)
childNode->Right->Parent = node;
childNode->Right = node;
childNode->Parent = node->Parent;
node->Parent = childNode;
return childNode;
}
Node* LR(Node* node)
{
node->Left = RR(node->Left);
return LL(node);
}
Node* RL(Node* node)
{
node->Right = LL(node->Right);
return RR(node);
}
Node* AVLSet(Node* node)
{
int depth = CalculateBalanceFactor(node);
if (depth >= 2)
{
depth = CalculateBalanceFactor(node->Left);
if (depth >= 1)
{
//LL : Left Left
node = LL(node);
}
else
{
//LR : Left Right
node = LR(node);
}
}
else if (depth <= -2)
{
depth = CalculateBalanceFactor(node->Right);
if (depth <= -1)
{
//RR : Right Right
node = RR(node);
}
else
{
//RL : Right Left
node = RL(node);
}
}
return node;
}
Node* Insert(Node* node, int data)
{
if (node == NULL)
{
node = (Node*)malloc(sizeof(Node));
node->Left = NULL;
node->Right = NULL;
node->Parent = NULL;
node->data = data;
return node;
}
else if (data < node->data)
{
node->Left = Insert(node->Left, data);
node->Left->Parent = node;
node = AVLSet(node);
}
else if (data > node->data)
{
node->Right = Insert(node->Right, data);
node->Right->Parent = node;
node = AVLSet(node);
}
else
{
//데이터가 중복되므로 추가하지 않는다.
}
return node;
}
Node* GetMinNode(Node* node, Node* parent)
{
if (node->Left == NULL)
{
if (node->Parent != NULL)
{
if (parent != node->Parent)
{
node->Parent->Left = node->Right;
}
else
{
node->Parent->Right = node->Right;
}
if (node->Right != NULL)
{
node->Right->Parent = node->Parent;
}
}
return node;
}
else
{
return GetMinNode(node->Left, parent);
}
}
Node* Delete(Node* node, int data)
{
if (node == NULL) return NULL;
if (data < node->data)
{
node->Left = Delete(node->Left, data);
node = AVLSet(node);
}
else if (data > node->data)
{
node->Right = Delete(node->Right, data);
node = AVLSet(node);
}
else
{
if (node->Left == NULL && node->Right == NULL)
{
node = NULL;
}
else if (node->Left != NULL && node->Right == NULL)
{
node->Left->Parent = node->Parent;
node = node->Left;
}
else if (node->Left == NULL && node->Right != NULL)
{
node->Right->Parent = node->Parent;
node = node->Right;
}
else
{
Node* deleteNode = node;
Node* minNode = GetMinNode(node->Right, deleteNode);
minNode->Parent = node->Parent;
minNode->Left = deleteNode->Left;
if (deleteNode->Left != NULL)
{
deleteNode->Left->Parent = minNode;
}
minNode->Right = deleteNode->Right;
if (deleteNode->Right != NULL)
{
deleteNode->Right->Parent = minNode;
}
node = minNode;
free(deleteNode);
}
}
return node;
}
void Inorder(Node* node)
{
if (node == NULL) return;
Inorder(node->Left);
printf("%d ", node->data);
Inorder(node->Right);
}
void main()
{
Node* root = NULL;
//INSERT
root = Insert(root, 4);
root = Insert(root, 10);
root = Insert(root, 13);
root = Insert(root, 20);
root = Insert(root, 25);
root = Insert(root, 32);
root = Insert(root, 55);
Inorder(root);
//결과 : 4 10 13 20 25 32 55 (root data : 20)
//DELETE
root = Delete(root, 4);
root = Delete(root, 10);
root = Delete(root, 13);
Inorder(root);
//결과 : 20 25 32 55 (root data : 25)
}
※ main 함수의 Insert를 보면 앞에서 다뤘던 이진탐색트리 때와는 다르게 수를 오름차순으로 넣어줘도 똑같은 트리가 만들어진 결과를 볼 수 있다.
※ Delete에서는 일부터 왼쪽 서브트리의 데이터를 모두 삭제했다. 그 결과, 리밸런싱을 통해 Root 노드가 25의 키값을 가진 노드로 변경이되어 양쪽 서브트리의 균형이 맞춰진걸 확인할 수 있다.
