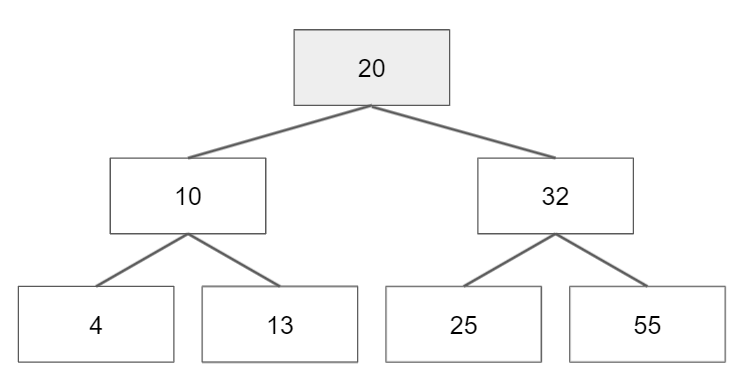
1. 힙(Heap)
- 최대값 혹은 최소값을 빠르게 찾아낼 수 있도록 고안된 완전이진트리 자료구조이다.
- 부모노드와 자식노드의 키 값 사이에 대소관계가 성립해야하는 조건을 만족해야한다.
- 부모노드의 키 값이 자식노드의 키 값보다 큰 힙을 '최대 힙', 반대를 '최소 힙'이라 부른다.
- 힙의 시간복잡도는 log n이다.
2. 코드
※ A-star pathfind에서 OpenList의 최소 F cost를 가진 노드를 가져오기 위해 적용한 Heap tree 코드이다.
※ 유튜브 영상에 있는 소스를 수정하여 사용했는데, 기존 코드는 배열을 사용하여 맵 사이즈만큼 할당하여 힙을 사용하고 있었다.
※ 그 결과, 실제로 맵 사이즈만큼의 할당이 필요없는데도 불구하고 많은 할당이 일어나 가비지가 많이 발생되므로 List로 변경하고 Capacity를 지정해줌. (만약의 경우 추가 할당이 필요한 경우가 있을 수 있으므로 List로 구성했다.)
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public interface IHeapItem<T> : IComparable<T>
{
int HeapIndex { get; set; }
}
public class HeapList<T> where T : class, IHeapItem<T>
{
private List<T> m_items;
public int Count => m_items.Count;
public int Capacity => m_items.Capacity;
public HeapList(int maxCapacity = 256)
{
m_items = new List<T>(maxCapacity);
}
public void Add(T item)
{
item.HeapIndex = m_items.Count;
m_items.Add(item);
SortUp(m_items[m_items.Count - 1]);
}
public void UpdateItem(T item)
{
SortUp(item);
}
private void SortUp(T item)
{
while(true)
{
int parentIndex = (item.HeapIndex - 1) / 2;
T parentItem = m_items[parentIndex];
if(item.CompareTo(parentItem) > 0)
{
Swap(item, parentItem);
}
else
{
break;
}
}
}
private void Swap(T itemA, T itemB)
{
m_items[itemA.HeapIndex] = itemB;
m_items[itemB.HeapIndex] = itemA;
int swapIndex = itemA.HeapIndex;
itemA.HeapIndex = itemB.HeapIndex;
itemB.HeapIndex = swapIndex;
}
public T GetRoot()
{
T rootItem = m_items[0];
//List의 원소가 1개일 때 List.Count로 원소를 가져오면 에러가 발생하므로 index값을 저장한다.
int lastIndex = m_items.Count - 1;
m_items[0] = m_items[lastIndex];
m_items[0].HeapIndex = 0;
m_items.RemoveAt(lastIndex);
SortDown(lastIndex);
return rootItem;
}
private void SortDown(int lastIndex)
{
int currentIndex = 0;
while(true)
{
int childLeft = currentIndex * 2 + 1;
int childRight = currentIndex * 2 + 2;
int swapIndex = currentIndex;
//왼쪽 자식 노드 유무 확인
if(childLeft < lastIndex)
{
swapIndex = childLeft;
//오른쪽 자식 노드 유무 확인
if(childRight < lastIndex)
{
//양쪽 자식 노드가 존재하면 두 자식 노드의 값을 비교해서 swapIndex 결정
//FCost 비교해서 오른쪽 자식노드가 작으면 swapIndex를 childRight로 변경해준다.
if(m_items[childLeft].CompareTo(m_items[childRight]) < 0)
{
swapIndex = childRight;
}
}
//현재 노드와 자식노드의 값을 비교해서 Swap
if(m_items[currentIndex].CompareTo(m_items[swapIndex]) < 0)
{
Swap(m_items[currentIndex], m_items[swapIndex]);
currentIndex = swapIndex;
}
else
{
return;
}
}
else
{
return;
}
}
}
public bool Contains(T item)
{
return item.HeapIndex >= m_items.Count ? false : Equals(m_items[item.HeapIndex], item);
}
}- GetRoot()로 루트노드를 힙에서 빼면 말단노드를 Root로 이동 후, 정렬(Sort down)한다.
- 노드를 추가하면, 말단노드에 추가한 뒤 정렬(Sort up)해서 노드의 위치를 지정해준다.
2-1) 힙을 사용하는 노드의 코드 (CompareTo() 구현)
public class Node : IHeapItem<Node>
{
private int m_hCost;
private int m_gCost;
private int m_heapIndex;
public int HeapIndex { get => m_heapIndex; set => m_heapIndex = value; }
public int FCost => m_hCost + m_gCost;
//Heap tree용 compare구현
public int CompareTo(Node other)
{
int compare = FCost.CompareTo(other.FCost);
if (compare == 0)
{
compare = m_hCost.CompareTo(other.m_hCost);
}
//힙에서 작은수가 루트로 올라가야하므로 -를 붙여서 반환한다.
return -compare;
}
}
※ 참고 유튜브 (맵 사이즈 만큼 배열을 할당하는 힙)
'Stack > Data struct' 카테고리의 다른 글
| C AVL 트리(AVL Tree) 구현 (2) | 2021.09.11 |
|---|---|
| C AVL 트리(AVL Tree) 설명 (0) | 2021.09.10 |
| C 트리 순회(Tree traversal) 구현 (0) | 2021.09.10 |
| C 이진탐색트리(Binary search tree) 구현 (0) | 2021.09.09 |
| C 트리(Tree) 설명 (0) | 2021.09.09 |